CRAC

Our goal is to solve scientific problems on an architecture composed of heterogeneous machines, widely distributed and linked by heterogeneous bandwidth. It is well known that direct methods are, most of the time, totally inefficient in such a context, since the total execution time is globally conditioned by the slowest machine and link. Furthermore, direct methods often use a lot of global communications (broadcast, gather-scatter, all-to-all, ...), which are a bottleneck on an heterogeneous network.

In fact, classical iterative methods suffer from the same problems, sometimes in worst when the convergence is particularly slow. Fortunately, there exists a class of iterative methods which is perfectly adapted to our execution context because it greatly reduces the need of synchronizations.

The two following sections illustrate these two classes of iterative algorithms: SIAC and AIAC. They show the first iterations of an abstract application as a Gantt chart, with 3 computing tasks A, B and C. In each case, we suppose that communications are asynchronous, that is non-blocking. It means that emission and reception of data can be done by the system while the application computes. Nevertheless, the code is based on the message passing paradigm which implies explicit routine calls to send and receive data from/to an application buffer.

SIAC stands for Synchronous Iterations, Asynchronous Communications. It is the classical way to implement parallel iterative algorithms.

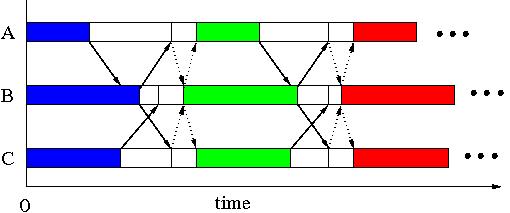
Plain boxes are computing time and white boxes idle times. Plain arrows represent the communications done at the end of each iteration to update the data of the neighbors. Dotted arrows represent the gather-scatter needed to check if the global convergence has been reached at the end of the current iteration. Obviously this test must be done after the data update, and at the end of each iteration. It leads to a lot of global communications and idle times.

back to top.

AIAC stands for Asynchronous Iterations, Asynchronous Communications.

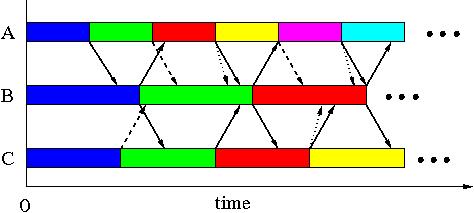
Plain boxes are computing time. Plain or hashed arrows represent the communications done at the end of each iteration to update the data of the neighbors. Dotted arrows represent communications concerning the local convergence state of a task. As we can see, the execution scheme is totally different from a SIAC since there are no idle times and global communications. Here is the sketch in three points:

• asynchronism : a task always starts a new iteration even if it did not receive data from its neighbors. For example, A receives data from B only during its third iteration.


• message crushing : if a task X receives several messages from the same task Y, concerning the same data to update, X can update with only the most recent message and crush the older ones. This mechanism is not mandatory but it greatly accelerates the convergence rate. For example, B receives two messages from A during its second iteration. The first one may be discarded (= hashed arrow).


• asynchronous convergence detection : as in SIAC, a task X is chosen to store (in an array) the convergence state of all tasks. Nevertheless, a task Y sends its convergence state only when it changes. At the end of each iteration, X checks for "convergence messages" from other tasks. If there are, it updates the array and checks if the convergence state of all tasks is true. If it is the case, the global convergence has been reached. If this state persists during few iterations, X warns all tasks to stop.
  For example, we suppose that A converges locally at the end of its third iteration. Then it sends a message to B. C does the same at the end of its third iteration. But A steps out its convergence state at the end of its fifth iteration, then it sends a new message to B to warn it. And so on until B detects the global convergence and warns A and C to stop.

Notes:

• Obviously, the same algorithm may be implemented in a SIAC or AIAC way. But if it is proven that the SIAC version will converge, the AIAC version may not. Thus, it is not possible to purely and simply apply AIAC technics to any algorithm.


• Fortunately, the convergence proof can be done by checking some mathematical properties on the iteration functions and can apply to a large class of scientific problems such as those described by a linear system involving M matrices or by partial differential equations.


• If the convergence is proved, the number of iterations needed to converge is higher for an AIAC execution than a SIAC one. Nevertheless, since there are no idle times, the total execution time is very often reduced, the gain depending on the algorithm, the data and the execution context.


• AIAC executions are tolerant to message delays (or lost): the execution keeps going on even if no update data are received.

back to top.

AIAC algorithms is a new way to address the efficiency problem on a Grid. Linking big clusters with very high speed networks is indeed a way but, from a pure computation point of view, it is just the same than using old parallel machines. The real challenge is to use hundreds of simple machines (even user machines) and to implement more efficient codes than those existing.
To summarize, it is time to leave the old manners for this credo: "adapt the algorithm to the Grid and not the opposite".

back to top.