Multiplication de matrice¶
Soit le produit de matrices \(C = A.B\) où
\(A = a_{i,j} (i \in [1;H], j \in [1;Q])\)
\(B = b_{i,j} (i \in [1;Q], j \in [1;W])\)
Le produit \(C = c_{i,j} (i \in [1;H], j \in [1;W])\) a pour éléments
\(c_{i,j} = \sum_{q \in [1;Q]} a_{i,q}b_{q,i}\)
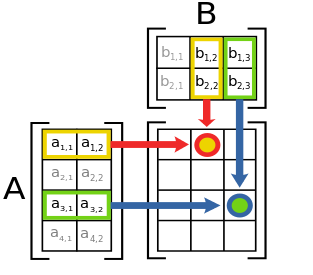
Illustration
Expérimentations
Écrire un kernel CUDA naif réalisant la multiplication parallèle de deux matrices. Pour ne pas compliquer trop la conception, on supposera que leurs dimensions sont des puissances de 2. On choisira comme niveau de parallèlisme : un thread calcule un coefficient du produit.
Écrire un programme main permettant d’exécuter la multiplication et mesurer les performances.
Le profileur nvprof permer de diagnostiquer les points faibles du programme. La documentation de nvprof est accessible ici. Il est possible de lister les grandeurs mesurables par
$ nvprof --query-metricsParmi ces grandeurs, on peut citer
gld_efficiency
gst_efficiency
shared_efficiency
shared_replay_overhead
global_replay_overhead
global_hit_rate
local_hit_rate
Expérimentations
Exécuter le programme au travers du profileur pour évaluer les performances du programme.
Déduire des pistes d’amélioration possibles.
Utilisation de la mémoire partagée¶
L’idée est de décomposer la matrice résultat en blocs rectangulaires ou carrés, associés aux blocs d’exécution GPU à raison d’un coefficient par thread. Les données d’entrée seront pré-chargées en mémoire partagée. Le calcul de la somme est alors effectué avec les valeurs rangées en mémoire partagée avant d’écrire le résultat final en mémoire globale.
Expérimentations
Écrire un nouveau kernel de mutliplication utilisant la mémoire partagée.
Mesurer les performances.