Matrix transpose

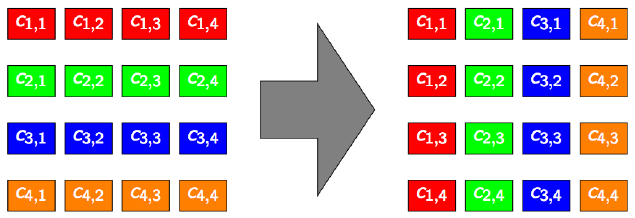
Let \(C\) be the matrix whose elements are denoted \(c_{i,j} (i \in [1;H], j \in [1;W])\).

The elements of the transposed matrix \(C^{T}\) are denoted \(c^{T}_{i,j} = c_{j,i} (i \in [1;W], j \in [1;H])\)

Example xhen \(H = W = 4\)

Naive transpose in global memory

Experiments

Design one CUDA kernel transpose_naive inside the template file. The kernel is intended to achieve the parallel transposition of any matrix with power-of-two dimensions. A code skeleton is available here (do not forget to rename this file before using it). A source file of the reference function is also available here.

This first transpose kernel just needs to achieve the matrix transpose, no performance tuning is expected. The whole computation can thus be done using only the GPU’s global memory.

Keep note of the mean execution time for one 4096 x 4096 integer elements matrix.

As a reminder, the main function does the following treatments:

• host-side (CPU) memory allocation for:

  • input data to be provided to the GPU,

  • output data to be copied back to CPU after kernel execution,

  • reference data to be compared to the GPU result in order to ensure that the GPU computation was correct.

• device-side (GPU) memory allocation for:

  • input data from CPU (matrix to be transposed),

  • output data (transposed matrix).

• input data generation, to fill in the matrix to be transposed. One can use random values but it may be smart to use well-chosen values in order to be able to judge the correctness just by displaying the output values.

• input data copy from CPU to GPU.

• grid and blocks dimensions setting.

• kernel execution.

• output data copy from GPU to CPU.

• result checking.

Note

• Debugging is one of the greatest difficulties when designing GPU programs.

• However, in the matrix transpose case, it is easy to write a non-parallel CPU reference (the provided compute_gold function).

Note

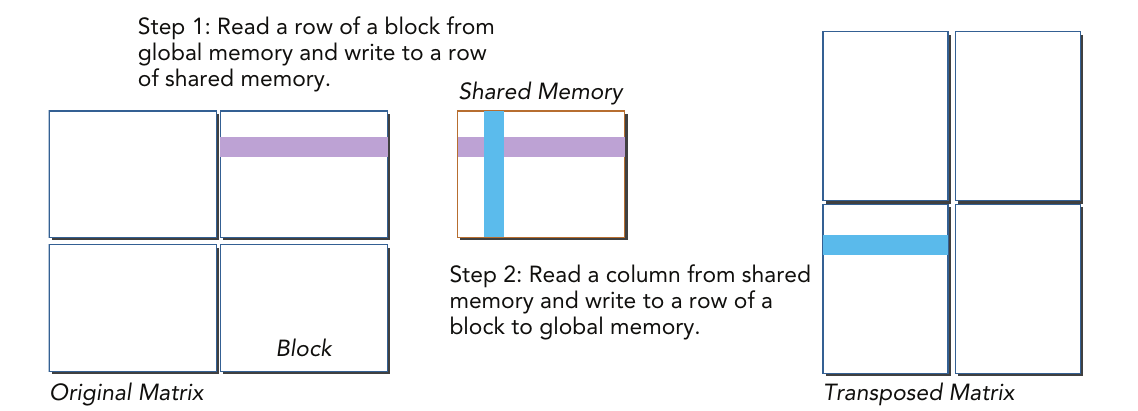
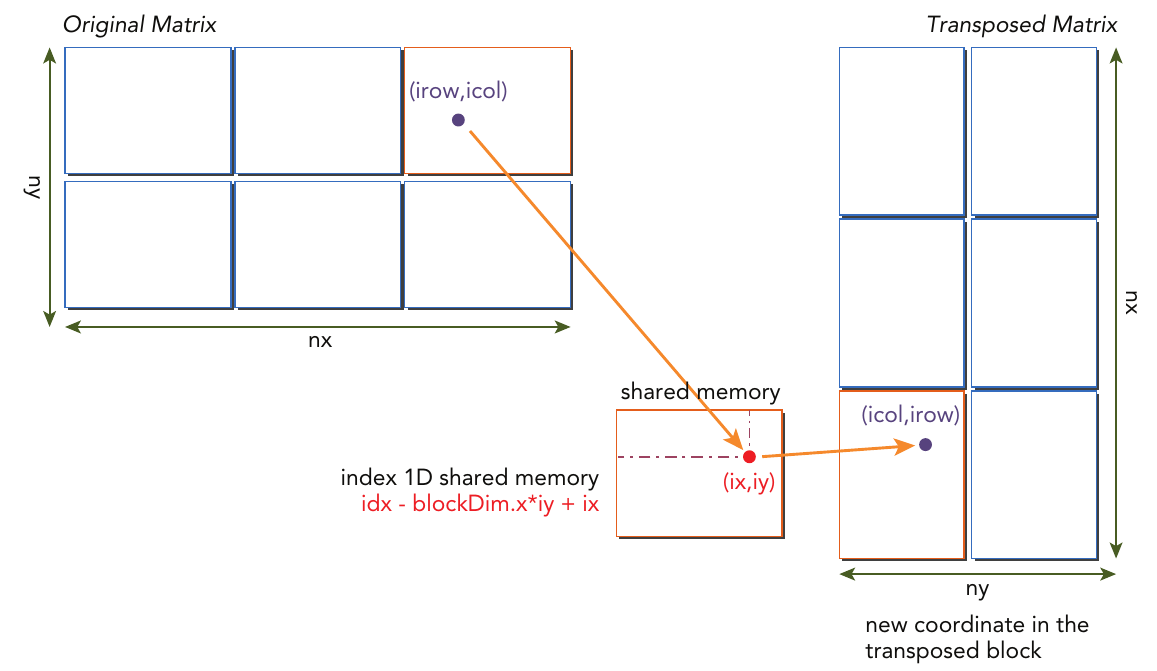
• the global memory read operation is coalesced within a warp (g_idata[i*j_dim +j]), while the global memory write operation exhibits strided access between neighboring threads. The performance for this naiveGmem kernel is a lower bound that progressive optimizations will be measured against.

Question

• Can you justify the fact that global memory write operation exhibits strided access between neighboring threads as said in the remark above?

Transpose using shared memory

To avoid strided global memory access, 2D shared memory can be used to cache data from the original matrix. A column read from 2D shared memory can be transferred to a transposed matrix row stored in global memory. While a naive implementation will result in shared memory bank conflicts, the performance will be much better than non-coalesced global memory accesses. The following figure shows the main idea of this kernel.

Experiments

• Design a GPU kernel transpose_shared_wbc that implements the above principle. It can be broken down into the following steps:

  1. A warp performs a coalesced read of a row from a block of the original matrix stored in global memory.

  2. The warp then writes the data into shared memory using row-major ordering. As a result, there are no bank conflicts for this write.

  3. After all read/write operations in the thread block are synchronized, you have a 2D shared memory array filled with data from global memory.

  4. The warp reads a column from the 2D shared memory array. Since the shared memory is not padded, bank conflicts occur.

  5. The warp then performs a coalesced write of that data into a row of the transposed matrix stored in global memory.

  Note

  • For each thread to fetch the right data from both global and shared memory, multiple indices must be calculated for each thread.

  • For a given thread, you first need calculate its coordinate in the original matrix based on its thread index and block index.

  • Then the index into global memory can be calculated.

  • Next the coordinates od the transposed matrix are calculated.

  • Finally, the index into global memory used to store the transposed matrix values can be calculated.

  The figure below details the process.

  

  • Compare the average execution time with the one of the naive kernel.

  • Modify the code to avoid shared memory bank conflicts (I have said a few words about this last week). You can call it transpose_shared_nobc.

Balancing the computation load and memory accesses

The process of transposing a matrix is clearly memory bandwidth bound, ie. it’s performance is limited by the memory accesses.

A commonly used approach to override such a limitation is to give more computation to each thread. In our case, one could imagine that each thread would transpose 4 or 8 elements instaed os just one. If all those elements belong to the same block, they are stored in shared memory during the data fetching step and thus, no additionnal memory access is generated.

Experiments

• Design a GPU kernel transpose_shared_nobc_balanced that implements the above principle with various thread loads (2, 4, 8, 16 elements).

• Compare the performance with the previous kernels.